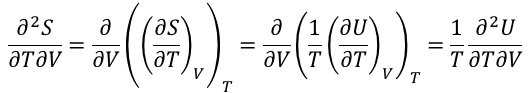ブログと仕事での文章の違い - 忘れん坊の外部記憶域

　ブログで毎日適当な文章をネット上に投稿している私ですが、仕事もデスクワークのため、毎日適当な文章を作成しています。

　ふと、ブログで書いている文章と仕事で書いている文章にどの程度差があるのか、気になりました。

　さっと比較をしてみたいところですが、よくよく考えなくてもメール本文や設計資料から文章を引用すると機密情報や企業ノウハウに抵触しかねません。

　ここは若手向けに作った私の教育資料から文章を抜粋してみましょう。教科書レベルの公知情報なので機密情報に触れるリスクはありませんし、昔作った資料なので書いた本人も何を書いたか忘れているため、比較にはちょうどいいです。

　つまり、今回は熱力屋さんや流体屋さん以外の全ての人を置いてけぼりにする記事です。「なんかよく分からんことを言ってるな」くらいに思っていただけますと。

気体の計算に関する若手向け教育資料から抜粋

[補足8]

摩擦、放熱などの若干の損失を伴う装置における気体の準静的過程の近似として用いるものをポリトロープ過程(ポリトロープ変化)という。

ポリトロープ指数mは変化の過程によって定まる。
　定圧過程：m=0
　等温過程：m=1
　可逆断熱過程：m=κ
　定積過程：m=∞
圧力と密度の関係式で表せるものをポリトロピックと言う。
実用的な考えとして「気体の準静的変化のことをポリトロープ変化という」と覚えてしまってもよい。

　想像以上に堅苦しい。そして学術的な厳密性を放り捨てた投げやりな教え方。ポリトロープ過程の学問的知見を教えたいのではなく実用上での理解を優先しているので勘弁願います。

　堅苦しい割に最後の一文は私らしい雑な感じがして、余計な個性を感じます。

不可逆断熱膨張に関する若手向け教育資料から抜粋

断熱膨張とジュール・トムソン膨張(不可逆断熱膨張)の違い
・可逆か、不可逆か(等エンタルピーか等エントロピーか)
・断熱膨張は温度が必ず下がるが、ジュール・トムソン膨張は下がるとは限らない
・理想気体でも起こるか、実在気体でしか起きないか

　雑な分類。

　冷蔵庫やエアコンが冷える原理を説明する入口ですが、説明の質は落第点。とはいえ入口からジュールトムソン係数の話をするのもアレですし、難しいところ。

　ちなみにジュールさんはエネルギーの単位ジュール[J]の元になった偉い人で、トムソンさんは温度の単位ケルビン[K]の元になった偉い人です。二人は熱力学の発展に多大な貢献をし、現代社会の礎を築いた偉大な科学者です。

[d、δの違い]
熱力的にはdは状態量(完全微分)、δは状態量ではない変化量(完全微分でない)。
例えば内部エネルギーの変化量dUは状態さえ決まれば一意に定まる。
対して外部とやり取りする熱量Qや仕事Wはある状態の系を見ても一意に定まらない。
つまり経路依存性(状態量か否か)を識別するためにdとδを使い分けている。

　数式の記号に関する説明。

　私が書いた文章だと一目で分かる[説明][例示][結論]の構成。教育資料だというのにカッコが多すぎて読みにくいのも特徴的。

　私は油断するとカッコまみれのカッコつけた文章を書きがちなので、ブログではなるべくカッコを付けないよう気を付けています。二重の意味で。

[偏微分と全微分]

流体は等方性(向きによって特性が変化しない)であることから、状態量はp,T,Vのうち2つが定まれば残り1つも自動的に定まる。理想気体の状態方程式pV=nRTのnとRがconstだと思えば分かりやすい。

このように多変数の方程式に対してその他の変数を固定して行う微分を偏微分という。記号はdではなく∂を使って区別する。

熱力学では固定した変数を右下に記載する表記が一般的。

これはTとpを固定してVでHを微分した、という意味。
何故かというと、熱力学では定積変化、定圧変化、断熱変化のように、ある変数を一定に保って固定したまま状態を変化させるという考えが重要なため。熱力で偏微分がやたら出てくるのはこのせい。

全部の変数で微分することを全微分(完全微分)という。完全微分が出来るということはその式が積分可能であることを意味する。つまり一意に定まる状態量として扱うことが可能。